Chapter 7: Results

7.1 Anthropometric Variables

Table 6.10 summarized the basic statistics for the anthropometric variables measured in this study. Tables 7.1 and 7.2 show the between- and within-family correlation matrices, respectively, for the anthropometric variables. The two correlation matrices are very similar. On average, the within family correlations are less than 0.14 smaller than the corresponding between family correlations (rbetween-family minus rwithin-family for each pair of variables) though there is some interesting variation to be discussed below. The Spearman rank-order correlation for the two data sets is rs = 0.85 (p< 0.0001), indicating that, for the most part, the pattern of relationships among the variables both between and within families is remarkably similar. This suggests that most of the between family correlations cannot be ascribed to between family environmental effects.

The exceptions are that overall body weight (BODY-WT) is significantly correlated with all three height measurements (total height: BODY-HT; sitting height: SIT-HT; and leg length: LEG-HT) between families but not within families (though the BODY-WT to SIT-HT correlation approaches significance within families). The correlations between fat-free weight (LBW) and the three height measurements show a similar pattern, even though the correlations with BODY-HT and SIT-HT are still significant. LBW to LEG-HT is not significant within families. Also of interest is the fact that SIT-HT and LEG-HT are moderately correlated between families but not within-families. These exceptions indicate that while some anthropometric variables are indeed correlated in the general

Table 7.1: Between family correlations among anthropometric variables 1

BODY-WT LBW BODY-HT SIT-HT LEG-HT ARM-CIRC TRICEPS

LBW .91**

BODY-HT .64** .70**

SIT-HT .56** .65** .77**

LEG-HT .55** .58** .93** .47**

ARM-CIRC .83** .70** .30 .26 .27

TRICEPS .65** .34* .18 .12 .17 .75**

% FAT .64** .27 .20 .06 .24 .65** .88**

* p<.05, ** p<.01

1All variables age corrected

Table 7.2: Within family correlations among anthropometric variables1

BODY-WT LBW BODY-HT SIT-HT LEG-HT ARM-CIRC TRICEPS

LBW .94**

BODY-HT .17 .32

SIT-HT .28 .38* .67**

LEG-HT .03 .15 .85** .17

ARM-CIRC .83** .69** -.04 .12 -.14

TRICEPS .82** .59** -.12 .05 -.20 .84**

% FAT .81** .59** -.11 .04 -.17 .86** .99**

* p<.05, ** p<.01

1All variables age corrected

population, the relationship may not be due to a genetic correlation (see below for a detailed discussion of methodological objections).

7.2 Neuroanatomical Variables

Table 6.3 provided the summary statistics for the neuroanatomical variables. These values are somewhat lower and more restricted in range than Wickett et al.'s (1994) sample of females which averaged 1250.5 cc with an SD of 94.1. The correlations between the basic neuroanatomic variables between-families (table 7.3) and within-families (table 7.4) have never been reported before to my knowledge. Of interest is the lack of a significant correlation between cerebral grey (GREYVOL) and white (WHITEVOL) matter. The within-family correlation is actually slightly negative (r= -0.10). Also of note are the relatively small correlations between the size of the brain stem + cerebellum (MMMVOL) and the other basic neuroanatomical divisions. Correlations with BRAINVOL are part/whole correlations, which can be quite high as a result (though this does not make them somehow invalid, of course).

Also of interest is that the estimated degree of tissue differentiation (EFFECT SIZE) is not significantly correlated with BRAINVOL, but is significantly positively correlated with WHITEVOL both between and within families. Thus, it would appear that individuals with greater white matter volumes also tend to have more distinct grey and white matter regions. Conversely, the negative correlations between EFFECT SIZE and GREYVOL (which reach significance within families) indicate that individuals with greater grey matter volumes tend to have less distinct grey and white matter regions. These findings suggest that additional white matter is added at the

Table 7.3: Between family correlations among neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL

PROSVOL .99**

GREYVOL .83** .84**

WHITEVOL .71** .73** .25

MMMVOL .66** .54** .48* .36*

EFFECT SIZE .07 .06 -.28 .48** .10

* p<.05, ** p<.01

1All variables age corrected

Table 7.4: Within family correlations among neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL

PROSVOL .99**

GREYVOL .73** .73**

WHITEVOL .59** .61** -.10

MMMVOL .63** .50** .42* .23

EFFECT SIZE -.08 -.05 -.63** .68** -.21

* p<.05, ** p<.01

1All variables age corrected

higher end of the distribution of pixel intensities, which moves the mean white matter value higher and thereby increases the value of EFFECT SIZE. Conversely, additional grey matter would appear to be added to the higher end of the grey matter distribution, which produces the opposite effect on EFFECT SIZE by moving the grey matter mean closer to the white matter mean. The significance of these findings is not completely clear, but they may indicate something about the basic structure of the brain, as discussed in the next chapter.

The correlation matrices for both within- and between family data are very similar, suggesting that between family sources of variance (e.g., cultural, socio-economic, etc.) do not significantly affect variability in these measures. The Spearman rank-order correlation between the within- and between-family correlations for the same variable pairs is quite strong (rs= 0.91, p< 0.0006), and the average difference between corresponding cells in the two correlation matrices is only 0.12 (rbetween-family minus rwithin-family for each pair of variables). These facts will also be important when considering technical reasons that might explain lower correlations within-families (e.g., due to range restriction and differential reliabilities of between- vs. within-family variables; see section on methodological objections below).

The between family correlations among neuroanatomical and anthropometric variables is shown in table 7.5. The correlations are very low, but tend to be positive (the negative correlations are tend to be small and none are significant). Only one correlation is significant at the p< 0.05 level (uncorrected for multiple comparisons): GREYVOL to SIT-HT. However, with the exception of WHITEVOL, all the volume measurements show positive associations with the various weight and height measurements. Across all comparisons, the average between-family

Table 7.5: Between family correlations of anthropometric and neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT SIZE

BODY-WT .16 .16 .14 .09 .15 -.11

LBW .17 .15 .20 -.01 .17 -.24

BODY-HT .22 .19 .29 -.05 .26 -.01

SIT-HT .28 .26 .39* -.02 .30 -.11

LEG-HT .14 .12 .16 -.05 .18 .05

ARM-CIRC .08 .07 -.03 .16 .11 .05

TRICEPS .00 -.02 -.12 .15 .10 .17

% FAT .09 .08 -.05 .24 .07 .19

* p<.05, ** p<.01

1All variables age corrected

Table 7.6: Within family correlations of anthropometric and neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT SIZE

BODY-WT .01 -.01 .12 -.15 .12 -.27

LBW .01 -.02 .09 -.15 .14 -.22

BODY-HT .06 .06 -.07 .09 .02 .10

SIT-HT .21 .19 -.02 .24 .22 .19

LEG-HT -.07 -.05 -.08 -.05 -.13 -.01

ARM-CIRC -.02 -.03 .20 -.27 .05 -.45**

TRICEPS .03 .02 .17 -.15 .08 -.35*

% FAT .00 -.01 .14 -.16 .05 -.34*

* p<.05, ** p<.01

1All variables age corrected

correlation is r= 0.10 (s= 0.13), which (assuming a normal distribution) is highly significant (p< 0.001).

The within-family correlations between neuroanatomical and anthropometric variables are shown in table 7.6. In contrast to the between family correlations, these are almost all close to zero. With respect to correlations in a positive direction, only that between SIT-HT and WHITEVOL approaches significance, though SIT-HT shows positive correlations greater than r= 0.20 with every neuroanatomical variable except GREYVOL. Overall, the average correlation in this table is r= -0.01, which is not significant.

The small size of the correlations between neuroanatomical and body size variables (particularly within families) indicate that body size corrections would not likely have a meaningful effect on the associations between brain variation and behavior. As was discussed in chapter 4, it is not at all obvious that one should a priori correct for body size when looking at associations between brain variation and behavior. Nevertheless, the brain/behavior results discussed below were repeated using BODY-WT and SIT-HT corrected neuroanatomical variables, and this was found to have only very slight effects on the correlation matrices, and no effect on the conclusions of this study.[1] Therefore, only the results calculated using neuroanatomical variables uncorrected for body size are reported below.

7.3 Cognitive Variables

The between and within family correlation matrices for the cognitive variables are shown in tables 7.7 and 7.8, respectively. These tables indicate a significant degree of positive association among all these variables (Bartlett's tests of sphericity: p<0.0001 for both within- and between-family matrices). None of the correlations, either between or within families, is significantly negatively correlated (at the p< 0.05 level[2]). The average correlation between families among these tests is r= 0.20, and the average within family correlation is r= 0.10. While these appear small, they are statistically highly significant. To illustrate this, a randomization study was carried out to determine the sampling distribution of the average correlation in a matrix of correlations based solely on random variables (using 12 variables with 36 cases each). The average correlation for each of 1000 different correlation matrices was calculated, and the average of these averages was found to be essentially zero (mean of mean r < 0.00006), while the standard deviation of these averages was s= 0.021. Thus, the within family average correlation obtained in this study of r= 0.10 is more than 4.7 standard deviations (p< 0.00001) away from what can be expected by chance alone, and the between family correlation is even more significant.

The overall pattern of correlations among the cognitive variables between and within families is similar but not identical. Of the 16 correlations which are significant between-families, five are also significant

within-families, with two more that just miss significance. Conversely, there are two correlations which are significant within families but not significant between families: MRT-SPEED to STROOP, and MRT-N to TRAILS. Another way to judge the overall similarity of the two matrices is to compare their first principal component loadings (first column of tables 7.7 and 7.8). The Spearman rank order correlation between these two sets of loadings is rs=0.58 (p=0.056). The rank-order correlation between corresponding correlations among the variables is low but still statistically significant (rs = 0.30, p< 0.02). Thus, they would appear to share a significant amount of internal structure, while at the same time exhibiting real differences in how cognitive tests intercorrelate within and between families.

RAVEN and SENTENCE-VERIF have the largest number of significant correlations both between and within families. The sizes of the correlations between RAVEN and VOCAB are similar, though smaller within families, again suggesting that the correlation between them cannot be explained by between-family sources of variance. This is consistent with, but does not prove, a genetic component to the association. If they were not correlated within families it would suggest an environmentally mediated correlation. In any case, this finding is significant because these two tests are most similar to the kinds of tests which are typical of standard IQ tests. It is also important to point out that they are very different kinds of tests on the surface: RAVEN is an entirely non-verbal abstract reasoning task, while VOCAB is completely verbal. Similarly, RAVEN and MRT-N, RAVEN and VERBALFL, as well as TRAILS and VERBALFL are all correlated significantly within and between families, yet these also are very different kinds of tasks that appear to require very different sorts of cognitive processing. Recall that MRT-N is a pure mental rotation (spatial) measure, TRAILS is a different sort of spatial measure that requires a simple form of planning and the ability to rapidly switch between over-learned sequences of symbols, and VERBALFL is entirely a measure of verbal fluency. All of this suggests that a significant degree of variance among very different sorts of cognitive tests is shared, both between and within families.

The average difference between the corresponding within and between family correlations is only 0.10 (SD = 0.24). If we can assume that the differences between the two sets of correlations should be normally distributed, we can calculate the probability of getting an average difference of 0.10 just by chance alone. Using a paired t-test, this turns out to be p< 0.001 (two-tailed). There are technical reasons to expect that within family correlations will be smaller than between family correlations (see below). It is likely that the between family values are more reliable population parameters, given that they are based on family averages.

7.4 Between-family Correlations of Cognitive Tests with Neuroanatomical Features

First, it is important to keep in mind that positive correlations between neuroanatomical variables and cognitive ability are probably more important that negative correlations with respect to understanding hominid brain size evolution. A negative correlation would imply that greater neuroanatomical volume leads to worse performance on some cognitive task. This would seem to be inherently problematic for understanding human neurocognitive evolution.[3]

Table 7.9 summarizes the zero-order between-family correlations of the cognitive test variables and the neuroanatomical variables (controlling for age and SIMPLE-RT). Only eight of the 66 correlations are negative, and none of these is larger than r= -0.12. The correlations of BRAINVOL with RAVEN, MRT-N, and TRAILS tests are statistically significant and similar to what has been found in previous MRI studies for IQ (which are the equivalent of between-family analyses with only one data point per family). The correlation of VOCAB with BRAINVOL is low compared to that found for a sample of 40 Canadian women by Wickett et al. (1994). This may be due to restriction of range in the present sample, given the high proportion of U.C. Berkeley students included, and the fact that the subjects completed an average of almost three years of college (table 6.2). MRT-SPEED correlation with BRAINVOL is higher than the value of r= 0.108 obtained by Wickett et al. (1994) for the pencil-and-paper version of the Vandenberg and Kuse Mental Rotation Test, but does not reach the p< 0.05 level of significance. This would suggest that speed of mental rotation, per se, is only moderately associated, if at all, with brain size. The significance of this finding for sex differences in brain size will be addressed in the next chapter. Given that MRT-N and MRT-SPEED are not significantly correlated with each other (either between- or within-families: see tables 7.7 and 7.8), and given that MRT-N is significantly correlated with RAVEN but not VOCAB, we may tentatively conclude that MRT-N is measuring some aspect of spatial processing or reasoning, but not speed of mental rotation itself. Of the four

Table 7.9: Between family correlations of cognitive to neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT SIZE

RAVEN .43** .40* .36* .29 .39* .22

VOCAB .14 .11 .07 .08 .20 -.03

MRT-SPEED .25 .22 .09 .27 .25 .15

MRT-N .44** .43** .22 .38* .31 .38*

STROOP .18 .20 .11 .23 -.02 .16

TRAILS .35* .33 .20 .30 .32 .20

VERBALFL .27 .25 .23 .15 .27 -.07

WCST-PERS .30 .24 .13 .29 .46** .26

OBJECT-ID -.08 -.12 -.06 -.10 .18 .12

SENTENCE-VERIF .26 .23 .22 .17 .28 .26

SYNTAX .22 .22 .31 -.01 .13 .05

* p<.05, ** p<.01, 1All variables corrected for age and Simple-RT.

Table 7.10: Between family correlations of neuroanatomic measures with cogntive 1st PC, and partial correlations with cogntive variables controlling for 1st PC1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT 1st PC

SIZE Loadings

1st PC .46** .42* .33 .32 .46** .27

RAVEN .07 .08 .15 .01 -.02 -.04 .88

VOCAB -.19 -.19 -.17 -.14 -.11 -.25 .60

MRT-SPEED .15 .13 .00 .21 .16 .09 .26

MRT-N .26 .27 .05 .26 .08 .29 .54

STROOP .12 .15 .06 .19 -.11 .12 .16

TRAILS .09 .09 -.02 .13 .04 .04 .65

VERBALFL .07 .06 .09 .00 .06 -.24 .48

WCST-PERS .12 .07 -.01 .17 .33 .16 .44

OBJECT-ID -.26 -.29 -.17 -.22 .05 .04 .30

SENTENCE-VERIF -.30 -.29 -.14 -.22 -.25 .06 .87

SYNTAX -.04 -.02 .17 -.23 -.17 -.12 .55

* p<.05, ** p<.01, 1All variables corrected for age and Simple-RT. The cognitive-to-neuroanatomic correlations are also corrected for 1st PC.

tests which generally show prefrontal specificity, only TRAILS was significantly associated with brain size.

Correlations with the neuroanatomical subdivisions of brain size show that the associations of BRAINVOL with RAVEN, MRT-N, and TRAILS are not due primarily to any one of the subdivisions. The correlations of these three cognitive measures are larger with BRAINVOL than with either GREYVOL, WHITEVOL, or MMMVOL. The average correlation between BRAINVOL and the 11 cognitive tests is r= 0.25. For GREYVOL the average correlation is r= 0.17, for WHITEVOL it is r= 0.19, and for MMMVOL it is r= 0.25. In only one case (MMMVOL to WCST-PERS) is there a significant correlation between a sub-component of BRAINVOL and a cognitive test that is not matched by a higher correlation with BRAINVOL itself.

The correlations with the degree of tissue differentiation (EFFECT SIZE) where moderate, with only MRT-N reaching significance. On average, EFFECT SIZE correlated with the 11 cognitive variables r= 0.15.

The loadings of the cognitive tests on the 1st PC, the correlations of the 1st PC to the anatomical variables, and the partial correlations of the other cognitive variables (controlling for the 1st PC) to the anatomical variables, are shown in table 7.10. The 1st PC, which explains more than 32% of the between-family variance in this sample, is significantly correlated with BRAINVOL (r= 0.46). This does not appear to be due exclusively or primarily to any single neuroanatomic sub-division. Overall BRAINVOL is more highly correlated with the 1st PC than are either GREYVOL or WHITEVOL (which both just miss significance at the traditional p< 0.05 level). MMMVOL is correlated with the 1st PC to the same degree as overall BRAINVOL, but since it represents only a small percentage of BRAINVOL, it alone cannot account for the overall correlation between BRAINVOL and 1st PC. EFFECT SIZE correlated with the 1st PC positively but does not reach statistical significance (r= 0.27).

As indicated in table 7.10, none of the partial correlations of the cognitive tests with BRAINVOL (controlling for 1st PC, age, and SIMPLE-RT) are significant. The same is true for all the other neuroanatomical variables, including EFFECT SIZE. Overall, 26 out of 66 associations are negative, and the average correlation for this table (excluding the 1st PC correlations) is only r= 0.01. This indicates that a single general cognitive dimension can account for the BRAINVOL correlation with the cognitive variables, and that little association is left after this dimension is accounted for. However, the partial correlation of WCST-PERS with MMMVOL just misses significance.

7.5 Within-family Correlations of Cognitive Tests with Neuroanatomical features

In contrast to the between-family correlations of brain size and the cognitive variables, the zero-order within-family correlations are mostly non-significant (table 7.11). The highest correlations with BRAINVOL were with the SENTENCE-VERIF and SYNTAX, but were not statistically significant. These two tests were the only ones to show consistently positive associations with the neuroanatomical variables, albeit at low levels. Recall that these tests also showed positive correlations with BRAINVOL between families: see above and table 7.9). The correlation between GREYVOL and MRT-SPEED was significantly negatively related within families (r= -0.49). MRT-SPEED was also negatively correlated with the BRAINVOL (r= -0.28),

Table 7.11: Within family correlations of cognitive to neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT SIZE

RAVEN -.08 -.07 .09 -.25 -.14 -.30

VOCAB .12 .12 .15 -.05 .04 -.16

MRT-SPEED -.28 -.27 -.49** .19 -.25 .52**

MRT-N .00 .01 .10 -.10 -.04 -.22

STROOP .08 .10 -.21 .43** -.03 .51**

TRAILS -.11 -.09 -.04 -.05 -.18 -.09

VERBALFL -.13 -.12 .08 -.27 -.09 -.25

WCST-PERS .09 .03 -.02 .03 .37* -.16

OBJECT-ID -.12 -.12 -.10 -.04 -.06 .09

SENTENCE-VERIF .22 .20 .16 .09 .23 -.05

SYNTAX .26 .27 .15 .24 .11 .24

* p<.05, ** p<.01, 1All variables corrected for age and Simple-RT.

Table 7.12: Within family correlations of neuroanatomic measures with cogntive 1st PC, and partial correlations with cogntive variables controlling for 1st PC1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT 1st PC

SIZE Loadings

1st PC -.05 -.03 .01 -.05 -.12 -.03

RAVEN -.07 -.06 .11 -.29 -.08 -.38* .67

VOCAB .15 .14 .15 -.03 .10 -.16 .39

MRT-SPEED -.28 -.27 -.52** .22 -.22 .56** .32

MRT-N .02 .02 .10 -.09 .00 -.23 .37

STROOP .11 .11 -.23 .48** .02 .57** .38

TRAILS -.10 -.09 -.05 -.03 -.14 -.09 .59

VERBALFL -.13 -.14 .09 -.33 -.01 -.32 .68

WCST-PERS .08 .02 -.02 .01 .35* -.18 -.34

OBJECT-ID -.12 -.13 -.13 -.02 .02 .14 .62

SENTENCE-VERIF .34* .29 .21 .17 .42* -.04 .67

SYNTAX .28 .28 .15 .26 .14 .25 .20

* p<.05, ** p<.01, 1All variables corrected for age and Simple-RT. The cognitive-to-neuroanatomic correlations are also corrected for 1st PC.

but positively correlated with WHITEVOL (r= 0.19), though the correlations were not significant in either case. WHITEVOL was significantly correlated with STROOP (r= 0.43), and MMMVOL was significantly correlated with WCST-PERS (r= 0.37). Since the probability values here are not corrected for multiple comparisons, it is very possible that these findings are due to sampling error.

All of the 1st PC correlations with neuroanatomical variables are very small (table 7.12), with none more positive than r= 0.01 (with WHITEVOL). The 1st PC accounts for 25% of the variation among the cognitive tests within families. The partial correlations of the cognitive variables with the neuroanatomic volume measurements (controlling for 1st PC) were mostly non-significant (table 7.12). However, the correlations between SENTENCE-VERIF and both BRAINVOL and MMMVOL are significant (without correcting for multiple comparisons). Overall, the correlations between SENTENCE-VERIF and SYNTAX remain positive for all volume comparisons (but the correlation between EFFECT SIZE and SENTENCE-VERIF is slightly negative: r= -0.04). These correlations suggest that some variance unique to these tests which is shared with brain volume measurements, though the possibility that this is simply error variance cannot be ruled out at this point.

It is possible to visualize the overall nature of the between- versus within-family difference in strength of associations by graphing the individual subjects and connecting respective pairs of sisters. Figure 7.1 demonstrates this comparison for the BRAINVOL to RAVEN association. The variables are uncorrected for age or SIMPLE-RT (unlike the correlations reported in tables 7.9-7.12) to simplify the graph and facilitate direct comparison with figure 5.2a and 5.2b. It is quite apparent from this figure

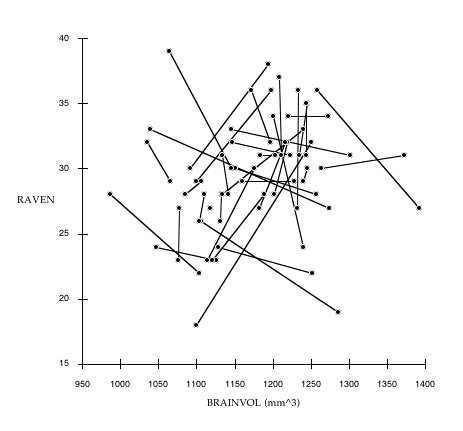
Figure 7.1: The association of BRAINVOL to RAVEN with family relationships indicated. Data points connected by lines represents sister pairs. The randomness of the within family relationships of the variables is immediately apparent (compare with figures 5.1A and 5.1B. For simplicity, these variables are not corrected for age or SIMPLE-RT.

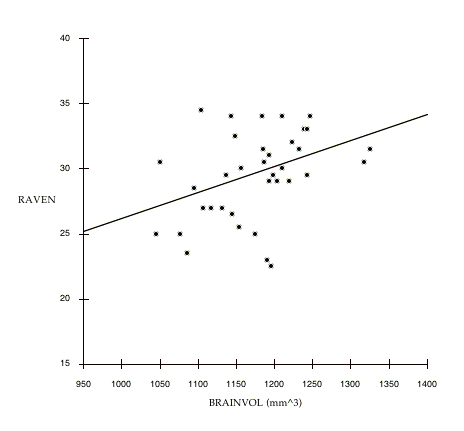
Figure 7.2: The between family relationship of BRAINVOL to RAVEN. Each data point represents the mean values for one pair of sisters. For simplicity, these variables are not corrected for age or SIMPLE-RT (the relationship is slightly stronger when calculated with corrected data). The line is a least squares regression: RAVEN = 6.191 + .02 *BRAINVOL, r = .39 (p < .05).

that the within family associations between these variables is close to zero: the slopes of the lines connecting sister pairs appear to be quite random, with numerous obvious cases in which the association is reversed within pairs. However, if we plot only the average values of BRAINVOL and RAVEN for each sister pair (figure 7.2), we find a correlation similar to the associations reported in other MRI/IQ studies reviewed in chapter 4. Note that the strength of the association between BRAINVOL and RAVEN is enhanced if we control for SIMPLE-RT and age (compare with table 7.9), suggesting that controlling for these variables is important.

7.6 Sociality

Table 7.13 shows that the between-family correlations of neuroanatomical variables with various sociality measures, as well as correlations with the first principal component of the first four sociality variables (SOCIALITY 1st PC), which accounts for 55% of the variance in these variables. These correlations are low but positive for all volume measures. None is significant except for the first principal component based on the first four sociality variables (SOCIALITY 1st PC). The highest correlations are generally found for MMMVOL and BRAINVOL, respectively, though not without exceptions (e.g., GREYVOL correlates with PEOPLE SEEN SOCIALLY r= 0.35).

The lowest correlations among the sociality measures are between the volume measurements and the subject's personal rating of their own degree of sociality (SELF RATING). This surely the most subjective of the sociality measures. Most subjects rated themselves about average with respect to sociality, which probably indicates they were either not willing or not able to

Table 7.13: Between family correlations of neuroanatomic to sociality measures1

SOCIALITY

EFFECT 1ST PC
BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL SIZE loadings2

ADDRESS BOOK .24 .19 .09 .20 .40* .09 .80

TOTAL

ADDRESS BOOK .23 .19 .02 .29 .34* .16 .77

RELATIVES

PEOPLE SEEN .32 .30 .35* .08 .28 .01 .64

SOCIALLY

PEOPLE TALKED TO .24 .21 .21 .10 .27 .24 .74

SELF RATING .04 .02 .01 .02 .14 -.11

RATING BY SIBLING .13 .12 .14 .06 .15 -.20

SOCIALITY 1st PC2 .34* .30 .21 .23 .44** .17

* p<.05, ** p<.01

1All variables corrected for age.

2Sociality 1st PC is based on the first four sociality measures only (see text).

Table 7.14: Within family correlations of neuroanatomic to sociality measures1

SOCIALITY

EFFECT 1ST PC
BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL SIZE loadings2

ADDRESS BOOK .06 .02 .05 -.02 .27 -.14 .67

TOTAL

ADDRESS BOOK .07 .04 .08 -.05 .21 -.29 .65

RELATIVES

PEOPLE SEEN .12 .12 -.01 .23 .07 .11 .74

SOCIALLY

PEOPLE TALKED TO .02 -.02 -.06 .09 .18 .07 .67

SELF RATING -.19 -.15 -.08 -.16 -.26 -.10

RATING BY SIBLING -.20 -.20 -.11 -.12 -.09 -.01

SOCIALITY 1st PC2 .10 .06 .02 .10 .26 -.08

* p<.05, ** p<.01

1All variables corrected for age.

2Sociality 1st PC is based on the first four sociality measures only (see text).

accurately judge themselves on this measure. The next lowest correlations were found with the sociality rating obtained on the subject by their sibling (RATING BY SIBLING). Thus, either this aspect of sociality is not very highly related to the neuroanatomical variables studied or the way it was measured is not very accurate. It was because of concerns such as these that SELF RATING and RATING BY SIBLING were not included in the calculation of SOCIALITY 1st PC.[4]

The corresponding within-family correlations, as shown in table 7.14, are all lower, on average by about 0.17 (excluding SOCIALITY 1st PC correlations). None of the correlations is significant; the highest being between MMMVOL and the ADDRESS BOOK and SOCIALITY 1st PC variables. The fact that the highest correlations between families also tended to be with MMMVOL may be of importance, but only further studies with larger sample sizes will be able to confirm this.

These results may be complicated by the fact that these measures show weak associations with the cognitive variables, but in opposite directions between families vs. within families. Table 7.15 shows the between family correlations of the sociality variables with the cognitive ones, including the 1st PC (which is derived from the cognitive variables) and SOCIALITY 1st PC (derived as described above). While only a few variables reach statistical significance, the overall picture suggests a positive association. The average correlation between ADDRESS BOOK TOTAL, PEOPLE SEEN SOCIALLY, PEOPLE TALKED TO, and the cognitive variables is r= 0.10 (which is

Table 7.15: Between family correlations of sociality with cognitive variables1

ADDRESS ADDRESS PEOPLE PEOPLE SELF RATING SOCIALITY

BOOK BOOK SEEN TALKED RATING BY 1st PC

TOTAL RELATIVES SOCIALLY TO SIBLING

RAVEN .32 .29 -.01 -.04 -.20 -.14 .21

VOCAB .06 .03 -.26 -.39* -.14 -.05 -.18

MRT-SPEED .18 .05 .06 .25 -.07 -.02 .18

MRT-N .09 .02 .22 .03 -.05 -.04 .12

STROOP -.21 .03 -.02 .22 .03 -.03 .00

TRAILS .41* .38* .25 .25 .10 .07 .44**

VERBALFL .28 .29 .10 -.01 -.14 -.21 .23

WCST-PERS .34* .30 -.12 .04 -.07 -.11 .21

OBJECT-ID .26 .22 -.28 .11 -.12 -.16 .13

SENTENCE-VERIF .29 .21 .15 .17 -.20 -.18 .28

SYNTAX .21 .20 .33* .18 .17 .08 .31

SIMPLE-RT .11 .10 -.18 .09 -.35* -.38* .05

1st PC (cognitive) .38* .32 .15 .07 -.05 -.05 .32

* p<.05, ** p<.01

1All variables corrected for age. 1st PC also corrected for SIMPLE-RT.

2Sociality 1st PC is based on the first four sociality measures only (see text).

Table 7.16: Within family correlations of sociality with cognitive variables1

ADDRESS ADDRESS PEOPLE PEOPLE SELF RATING SOCIALITY

BOOK BOOK SEEN TALKED RATING BY 1st PC

TOTAL RELATIVES SOCIALLY TO SIBLING

RAVEN -.14 -.05 -.18 -.27 .20 -.09 -.23

VOCAB -.47** -.21 -.25 -.24 .03 -.07 -.42*

MRT-SPEED -.44** -.32 .03 .08 -.15 -.25 -.22

MRT-N -.20 .00 .04 -.11 .19 .14 -.09

STROOP -.14 -.16 -.11 -.14 -.11 .00 -.20

TRAILS .06 .03 .02 -.09 .04 .15 .01

VERBALFL -.01 .02 .08 -.08 .22 .16 .01

WCST-PERS .06 .14 -.08 -.15 -.38* -.38* -.01

SIMPLE-RT .08 .12 -.30 .00 .15 .10 -.05

OBJECT-ID .14 .18 .12 .02 .04 .03 .17

SENTENCE-VERIF .05 .12 -.06 -.11 -.17 -.13 .00

SYNTAX -.21 -.21 .02 .13 -.09 -.27 -.09

1st PC (cognitive) -.16 -.05 -.03 -.15 .11 .03 -.14

* p<.05, ** p<.01

1All variables corrected for age. 1st PC also corrected for SIMPLE-RT.

2Sociality 1st PC is based on the first four sociality measures only (see text).

significantly greater than zero[5]). The correlation between SOCIALITY 1st PC and the cognitive 1st PC just barely misses significance at the p< 0.05 level.

By contrast, table 7.16 shows the same correlations derived for within family comparisons. In this case the pattern is reversed, with an abundance of weak negative correlations. The average correlation (within families) between ADDRESS BOOK TOTAL, PEOPLE SEEN SOCIALLY, PEOPLE TALKED TO, and the cognitive variables is r= -0.10 (which again is significantly greater than zero, but in the opposite direction). This pattern suggests that although there is a weak association between cognitive performance and sociality (as measured in this study) in general, within families one sibling tends to take a more academic role while the other takes a more social role. This suggests that some portion of variability in the sociality measures (and/or the cognitive variables) is affected by environmental effects that are unique to a family unit.

7.7 Rate of Maturation

As indicated in table 7.17, the age at maturation does not have a significant positive correlation with any neuroanatomical variable either between- or within-families. In fact the correlations within-family are all slightly negative, with the MENARCHE to MMMVOL correlation reaching statistical significance. Thus, the effect of brain size on maturation is not obvious within humans, even though it is highly significant between species and has important evolutionary implications (as indicated in chapter 5). This may be a key finding, because of all the behavioral measures

Table 7.17: Between and within family correlations of MENARCHE with neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT SIZE

BETWEEN .07 .13 .13 .13 -.23 .10

WITHIN -.29 -.25 -.16 -.17 -.36* -.03

* p<.05, ** p<.01

1All variables age corrected

Table 7.18: Between and within family correlations of THROW (throwing accuracy) with neuroanatomic variables1

BRAINVOL PROSVOL GREYVOL WHITEVOL MMMVOL EFFECT SIZE

BETWEEN .05 .03 .06 -.08 .15 -.03

WITHIN .01 .03 .08 .00 -.07 .12

* p<.05, ** p<.01

1All variables age corrected

Table 7.19: Estimated effect of range-restriction and reliability differences on the largest associations with BRAINVOL found in this study 1

F ratio* rbetween rwithin actual p*** estimated estimated

equivalent rwithin absolute % of actual

after difference difference

corrections** explained explained

RAVEN 1.55 .43 .28 -.08 <.01 .15 29%

TRAILS 2.19 .35 .20 -.11 <.02 .16 34%

MRT-N 1.39 .44 .29 .00 <.02 .15 34%

1See text for explanation and formulas used in to make these calculations.

*F ratio = (between family variance)/(within family variance) for the cognitive variables (uncorrected for age or SIMPLE-RT. The F ratio for BRAINVOL in this study is 2.248.

**These calculations assume the following reliabilities for the variables: BRAINVOL rxx=.95, RAVEN rxx=.80; TRAILS and MRT-N rxx=.70.

***The probability that actual rwithin is as large as the estimated rwithin equivalent after corrections.

investigated in this study, MENARCHE is arguably the most directly comparable across species. If there is no demonstrable correlation for MENARCHE (either within- or between-families), there may be no reason to expect the cognitive variables to show correlations either.

7.8 Throwing Accuracy

As seen in table 7.18, throwing accuracy (THROW) is not significantly correlated with any neuroanatomical variable measured in this study, either between or within families.

7.9 Methodological Issues

Before accepting at face value the lack of a within-family correlation between general cognitive ability (as gauged by the 1st PC) and brain size (as well as the general lack of significant correlations between the cognitive and neuroanatomic variables), it is important to address the question of whether (and to what extent) these findings are attributable to the methodology used in this study. Since between family correlations are calculated from the mean sibling values in each family on the variables of interest, while the within family correlations are calculated using the signed sibling differences, how can we be confident that the differences in results are not due simply to the methodology? There are several lines of evidence, outlined below, which indicate that these methodological issues are not the cause of the differences obtained for between family and within family correlations.

7.9.1 Reliability Differences and Restriction of Range

There are two known statistical effects which might contribute to lower within-family than between-family correlations. The first has to do with the fact that the reliability of a measurement based on differences is less than the reliability of one based on averages (Jensen 1980). Since the correlation of one variable with another cannot be higher (barring sampling error) than the geometric mean of the reliabilities of these variables, and since (everything else being equal) within-family variables tend to be less reliable than between-family variables, we should expect within-family correlations to be less than between-family correlations. However, it is possible to estimate the expected size of this effect for a given size correlation if we can estimate the reliability of the original variables and the within-family (or intraclass) correlations for them.

The size of a correlation is also affected by the extent to which the range of the variables is restricted. The more we restrict the range of one variable, the lower we can expect the correlation to be with another variable. As was pointed out in section 6.2.5.2 (and see appendix C), the intraclass correlations for the variables in this study (particularly some of the cognitive ones) are low, indicating that a relatively larger proportion of variance is found within-families. Restriction of range among the overall sample will have the expected effect of decreasing the ratio of between-family to within-family variance. This is because the within-family variance will not be affected by this sort of sampling bias, but the between-family variance of the sample will decrease relative to the population at large. Equations exist which allow one to estimate the expected size of this effect, assuming one has an idea of the extent of the restriction in range. We are interested here in estimating whether or not the difference in the amount of variance within- versus between-families might explain the difference in the size of the correlations found within- versus between-families. In the present study, BRAINVOL between-families has a standard deviation of 93 cm3, which is significantly different from the within-family standard deviation of 62 cm3.[6]

To estimate the combined effect of these factors on the present data set, the following procedure was used: First, since the range restriction formula assumes no differences in reliability in the two samples, the between family correlation was corrected for attenuation due to imperfect reliability.[7] Second, this corrected between-family correlation was used (with knowledge of the degree of range restriction in BRAINVOL within- vs. between-families for this sample) to estimate what the within-family correlation would be if the only reason for the difference was a restriction of range.[8] Finally, the resulting within-family estimate (which assumes no attenuation) was attenuated to make it comparable to the original between- and within-family correlations.[9] This leaves us with an estimate of what the within-family equivalent would be of a between-family correlation, assuming that restriction of range and differences in reliabilities were the only reasons for the difference.

As it turns out, these two technical effects appear to account for only a relatively small portion of the observed difference. Table 7.19 shows the estimated within-family equivalents for the three variables with the largest between-family associations with BRAINVOL. These calculations were made using reasonable assumptions about the size of the reliabilities of various cognitive measures and of BRAINVOL, and use the measured degree of restriction of range in BRAINVOL (see footnote 26). As is evident, only about 0.15 (or ~one third) of the difference of the within- compared to the between-family correlations can be explained by the combination of these corrections. The probability that empirically derived within-family correlations are as large or larger than the estimated within-family equivalents (which assume only range-restriction and reliability differences) are all less than p< 0.05. The 95% confidence intervals for the actual within-family correlations do not overlap with the estimated within-family equivalents which assume only restriction of range and attenuation differences (as derived above). These calculations suggest that range-restriction and attenuation differences account for only a portion of the difference found in the between- versus within-family correlations.

7.9.2 Empirical Relationship Between Variance Differences and the Differences in the Size of Correlations

We can also directly assess the effect of range restriction in the actual data by calculating the relationship between: 1) the degree of range-restriction in different variables, and 2) the degree to which these variables show greater between-family than within-family correlations. If range-restriction were a significant factor, we should find that those variables displaying the greatest degree of range restriction within families should also tend to show the largest difference between the two types of correlations. Figure 7.3 shows this relationship for the 12 cognitive variables used in the present study. It is apparent that the degree of range restriction (as gauged by the F ratio of the between-family to within-family variance) explains essentially none of the variability in the difference of between vs. within family correlations (averaged across the four independent neuroanatomical variables: GREYVOL, WHITEVOL, MMMVOL, EFFECT SIZE). The slope of the regression line suggests that (on average for these variables) the difference of within vs. between family correlations does not change when increasing the proportion of between family to within family variance. For these variables and these data, range-restriction does not appear to explain the lower within-family correlations.

7.9.3 Randomization Studies

Another way to test for methodological artifacts is to carry out randomization studies. One approach is to calculate the within vs. between family correlations on sets of random variables. This will allow the estimation of the chances of getting a difference between vs. within family

correlations purely by chance. Four random sets of 36 numbers were assigned to the following variables: Xsib1, Xsib2, Ysib1, Ysib2. Variable Xsib1 represented the scores of the first sibling on test X, Ysib1 represented the scores of the first sibling on test Y, and so forth. Between and within family data sets were calculated in exactly the same manner as described above, and correlations were then calculated for the variables X and Y using both the family averages (i.e., mean of Xsib1 and Xsib2; mean of Ysib1 and Ysib2) and the signed within-family differences (i.e., Xsib1 minus Xsib2, and Ysib1 minus Ysib2). Then the signed difference between the within- and the between-family correlations was calculated. This whole process was repeated 1000 times to estimate the chances of getting a difference between vs. within families of at least 0.51, as was found in the present study for BRAINVOL to 1st PC.

The results were as follows. The average between-family minus within-family difference was only +0.007 (SD = 0.237).[10] Only 14 trials (p= 0.014) resulted in a difference of ³ +0.50. This shows that the basic methodology of calculating between and within family correlations, as used on the empirical data in this study, does not in and of itself result in higher between family compared to within family correlations. The randomization study also resulted in an average between-family correlation of -0.0002 (SD = 0.172). Only 5 trials (p= 0.005) resulted in a between family correlations of ³ 0.46 (found for BRAINVOL to 1st PC in the present study).[11] This further confirms that the between family correlation obtained in this study between BRAINVOL and 1st PC is highly significant.

This randomization study does not, however, deal with the question of different reliabilities of between and within family correlations. Another way to address this question is to repeat the methodology on random pairings of the actual data, which of course have less than perfect reliabilities. This will allow us to see whether there is something unique about the true pairing of siblings, independent of the methodology. Each sibling was therefore randomly paired with some individual other than her true sibling. Within and between group (they are no longer family pairs) correlations were calculated in exactly the same manner as described above (including age and SIMPLE-RT correction, calculation of 1st PC, and calculation of the 1st PC to BRAINVOL correlation both within and between groups), and the between group minus within group correlation differences were calculated for these two variables. Thus, this randomization study included all aspects of the methodology. This whole process was repeated 101 times to estimate the range of possible results.

It was found that the average difference of between- minus within- group correlations for BRAINVOL to 1st PC was only .11 (s= 0.23).[12] A difference greater than the actual difference obtained for true family pairings occurred in only 5 random pairings out of 101 (p< 0.05). Notice that these results agree with the calculations in table 7.19 that estimate the size of the range-restriction and reliability differences effects on these data. Figure 7.4 shows the histograms of the within- and between-pair calculations for these 101 random pairings, along with a histogram of the differences for each random pairing of the between-family minus within-family difference. The actual sibling-pair values are shown for comparison, along with the probabilities (one-tailed) that the sibling-pair values could have been the result of random pairings (these calculations assume a normal distribution).

Thus, randomization studies also suggest that the methodology alone cannot explain the lack of correlation within families of BRAINVOL to 1st PC. Pairing siblings together has the unique effect of eliminating within-group correlations between brain anatomy and cognitive ability. This fact is very difficult to explain as a simple side effect of the methodology used in this study.

7.9.4 Consistency Across Subsets of Data

If the methodological differences in the way between and within family correlations are calculated explain the differences in size of correlations, we should also expect this to be a widespread pattern for all the between vs. within family comparisons, not just the neuroanatomical vs. cognitive test comparisons. However, significantly lower within family correlations seem to mostly be associated with comparisons of neuroanatomical to cognitive variables, not with neuroanatomical to neuroanatomical, cognitive to cognitive, or anthropometric to

anthropometric comparisons. For example, RAVEN and VOCAB, two very different kinds of tests, correlate significantly both within and between families, and the difference in the size of the correlations is only .14 (rwithin= 0.40, rbetween= 0.54; see tables 7.7 and 7.8). Similarly, GREYVOL and MMMVOL, two independent subsets of brain tissue, show a similar pattern (rwithin= 0.42, rbetween= 0.48; see tables 7.3 and 7.4).

Overall the between and within family correlation matrices for neuroanatomical variables (tables 7.3 and 7.4) are very similar to each other. On average, the within family correlations are only 0.12 smaller than the corresponding between family ones. The average difference of corresponding between vs. within family correlations for cognitive variables is only 0.10 (tables 7.7 and 7.8). The same pattern is found among the anthropometric variables (tables 7.1 and 7.2), for which the average difference is 0.14. Note that these values correspond nicely to the results of the second randomization study reported in the previous section. It is also no doubt true that some of the cognitive to cognitive, neuroanatomical to neuroanatomical, and anthropometric to anthropometric comparisons include cases in which the two variables really are not correlated significantly or as highly within families, even if they are correlated between families. For this reason these average differences found for neuroanatomical to neuroanatomical, cognitive to cognitive, and anthropometric to anthropometric comparisons should be considered the high end of any estimated methodological effect.

By contrast, the average difference for the BRAINVOL to cognitive variable correlations is 0.25 (the overall average difference for all the neuroanatomical to cognitive correlations is 0.21). The difference tends to be even larger for those tests (e.g. RAVEN) that load highly on the 1st PC. This is reflected in the fact that the difference between vs. within family for the BRAINVOL to 1st PC correlations is 0.51. Across all the neuroanatomical volume to 1st PC correlations the average difference is 0.45 (the EFFECT SIZE correlations with 1st PC differ by 0.30 between vs. within families; compare tables 7.9 and 7.11). This pattern is difficult to explain solely in terms of range-restriction and reliability differences (or other methodological issues) between the two sets of variables.

7.9.5 A Note About Age Correction

The analyses reported here were repeated with non-age-corrected variables, and no significant differences in results were found. Analyses were also repeated on data in which age correction had been done on the 72 individuals first (before calculating within- and between-family values), and again no significant differences in results were found.

7.9.6 Summary of Methodological Issues

As indicated above, there are a variety of reasons to doubt that methodological differences and/or statistical artifacts play a significant role in explaining the lower correlations of neuroanatomical vs. cognitive ability within- compared to between-families, though there appears to be a small affect (the expected difference in size of the correlations is less than about 0.15).

7.10 Mean Differences in Behavioral Variables Between Larger- and Smaller-Brained Siblings

A more basic way of addressing the central issue of whether brain anatomy differences are associated with behavioral differences is to compare larger- and smaller-brained siblings on the behavioral variables. This is similar to the methods used to show that myopia is associated with IQ within families (Cohn et al. 1988), as discussed in chapter 5. It is possible (though unlikely) that even though the within-family correlations are very low, there might exist mean differences in behavior between larger- and smaller-brained siblings. On average, sibling pairs differed in BRAINVOL (corrected by age and SIMPLE-RT) by 65.7 cc (s=58.7 cc), with a range of 1.0 cc to 237.8 cc. Table 7.20 shows the mean differences for the 11 cognitive tests (also corrected for age and SIMPLE-RT[13]) between the larger and smaller BRAINVOL sibling. The differences are calculated by subtracting the smaller-brained sibling's cognitive test score from the larger-brained sibling's score, and averaging for all pairs. The mean differences in this table (and subsequent tables of this type) are not standardized: they retain their original units. Thus, they are not directly comparable to each other (e.g., RAVEN is scored as the total number of correct items, whereas SYNTAX is measured in milliseconds), but are included to give one an idea of the magnitude of the differences (for example, table 7.20 shows that larger brained siblings answered correctly, on average, .61 questions more than their smaller brained siblings). For direct comparison to other cognitive tests and variables, t-values are shown, which are the mean differences standardized by the standard errors of these mean differences. One-tailed probabilities are

Table 7.20: Average within-family differences for the cognitive variables in this study

Mean

Variable1 N Difference2 SD t-Value3 Probability4

RAVEN 36 .61 4.74 .77 NS

VOCAB 36 .87 5.93 .88 NS

MRT-SPEED 36 -.08 .44 -1.12 NS

MRT-N 36 .43 4.11 .62 NS

STROOP 36 .96 10.21 .57 NS

TRAILS 36 -.53 10.10 -.31 NS

VERBALFL 36 -.05 12.36 -.02 NS

WCST-PERS 36 2.11 15.32 .83 NS

OBJECT-ID 36 -29.77 172.94 -1.03 NS

SENTENCE-VERIF 36 176.72 899.54 1.18 NS

SYNTAX 36 225.92 935.10 1.45 p<.10

SIMPLE-RT 36 .01 54.51 .00 NS

1Corrected for age and SIMPLE-RT, except SIMPLE-RT itself, which is only age corrected.

2Mean of (larger-brained sister's score) - (smaller brained sister's score) for each variable

3(Mean Difference)/4One-tailed

Table 7.21: Average within-family differences for the First PC, and the other cognitive variables controlling for First PC Mean

Variable1 N Difference2 SD t-Value3 Probability4

1st PC 36 .05 1.00 .31 NS

RAVEN 36 .44 3.52 .75 NS

VOCAB 36 .75 5.48 .82 NS

MRT-SPEED 36 -.09 .42 -1.30 NS

MRT-N 36 .35 3.83 .54 NS

STROOP 36 .76 9.44 .48 NS

TRAILS 36 -.84 8.09 -.62 NS

VERBALFL 36 -.49 9.01 -.33 NS

WCST-PERS 36 2.39 14.32 1.00 NS

OBJECT-ID 36 -35.48 132.74 -1.60 NS

SENTENCE-VERIF 36 144.64 666.01 1.30 NS

SYNTAX 36 215.80 917.36 1.41 p<.10

11st PC is independent of age and SIMPLE-RT. Other variables controlled for age, SIMPLE-RT, and 1st PC

2Mean of (larger-brained sister's score) - (smaller brained sister's score) for each variable

3(Mean Difference)/4One-tailed

shown (uncorrected for multiple comparisons). As is evident from this table, the mean differences on the cognitive tests are very small, though 8 of the 12 tend in the direction favoring the larger brained sibling (i.e., the t-values are positive). Only one of these mean differences (that for SYNTAX) approaches significance.

Table 7.21 shows the same calculations for 1st PC, as well as for the cognitive tests in which variance associated with 1st PC and SIMPLE-RT has been removed. Essentially the same results are obtained as in table 7.20. Table 7.22 shows the values for MENARCHE, THROW, and the sociality measures, again with null results (and several displaying the opposite pattern that would be predicted if BRAINVOL had some positive effect on them.

For completeness, the same analyses were carried out after dividing the sister pairs into three equal sized groups which differ in their average within-pair BRAINVOL differences. In the group with the largest BRAINVOL differences, the sisters differed by 132.2 cc (SD=43.2). The middle group had an average sister difference of 53.9 cc (SD=17.6). The last group differed by only 10.6 cc on average (SD=7.5). Again, if BRAINVOL had some effect within families, we would expect it to be most pronounced in the group with the largest within-pair BRAINVOL differences. Table 7.23 lists the mean differences and associated t-values for the cognitive tests controlling for age and SIMPLE-RT. Once again, none of the mean differences were significant at the p<0.05 level (thought the sample sizes are lower, of course). Furthermore, there is no consistent pattern in which the group showing the largest sibling differences in BRAINVOL tended to show the largest differences in the cognitive test scores. Only six of the 11 cognitive tests show positive t-values (indicating that the larger BRAINVOL

Table 7.22: Average within-family differences for MENARCHE, THROW, and sociality measures

Mean

Variable1 N Difference2 SD t-Value3 Probability4

MENARCHE 35 -.12 1.26 -.55 NS

THROW 36 -.56 4.26 -.79 NS

Sociality measures:

ADDRESS BOOK TOTAL 36 .04 50.10 .01 NS

ADDRESS BOOK RELATIVES 36 .64 6.90 .56 NS

PEOPLE SEEN SOCIALLY 36 .18 16.15 .07 NS

PEOPLE TALKED TO 36 -3.64 49.62 -.44 NS

SELF RATING 36 -.12 1.33 -.55 NS

RATING BY SIBLING 36 -.40 1.38 -1.76 NS

SOCIALITY 1st PC5 36 .01 1.00 .07 NS

1Corrected for age. THROW is also corrected for SIMPLE-RT

2Mean of (larger-brained sister's score) - (smaller brained sister's score) for each variable

3(Mean Difference)/

4One-tailed

5Based on first four sociality measures only (see text)

Table 7.23: Average within-family differences for the cognitive variables in this study grouped by within-family BRAINVOL differences

Sibling BRAINVOL Mean Difference

Variable1 Difference2 N on Variable3 SD t-Value4 Probability5

VOCAB largest 12 1.79 7.65 .81 NS

middle 12 1.93 5.68 1.18 NS

smallest 12 -1.11 3.85 -1.00 NS

RAVEN largest 12 .09 6.14 .05 NS

middle 12 .02 4.37 .01 NS

smallest 12 1.71 3.56 1.67 p<.10

MRT-SPEED largest 12 -.28 .43 -2.28 NS

middle 12 -.02 .40 -.15 NS

smallest 12 .05 .46 .37 NS

MRT-N largest 12 .71 5.46 .45 NS

middle 12 .57 3.60 .55 NS

smallest 12 .00 3.27 .00 NS

STROOP largest 12 1.63 10.66 .53 NS

middle 12 -.29 7.12 -.14 NS

smallest 12 1.55 12.85 .42 NS

TRAILS largest 12 -.16 12.46 -.04 NS

middle 12 -2.22 9.87 -.78 NS

smallest 12 .80 8.16 .34 NS

VERBALFL largest 12 -.58 13.36 -.15 NS

middle 12 -2.50 13.35 -.65 NS

smallest 12 2.93 10.64 .95 NS

WCST-PERS largest 12 -.96 12.12 -.27 NS

middle 12 8.42 16.36 1.78 p<.10

smallest 12 -1.13 16.34 -.24 NS

OBJECT-ID largest 12 -28.27 197.51 -.50 NS

middle 12 -19.66 156.23 -.44 NS

smallest 12 -41.39 177.43 -.81 NS

SENTENCE-VERIF largest 12 231.25 1198.67 .67 NS

middle 12 293.52 658.23 1.54 p<.10

smallest 12 5.38 808.95 .02 NS

SYNTAX largest 12 297.09 1309.86 .79 NS

middle 12 132.35 887.24 .52 NS

smallest 12 248.32 513.48 1.68 p<.10

1Corrected for age and SIMPLE-RT

2Divided into equal thirds. The groups showed the following within-family differences in BRAINVOL (corrected for within-family age differences): largest: 132.2 cc (SD=43.2); middle: 53.9 cc (SD=17.6); smallest: 10.6 cc (SD=7.5).

3Mean of (larger-brained sister's score) - (smaller brained sister's score) for each variable

4(Mean Difference)/

5One-tailed

sibling also tended to score higher on the cognitive test).

Table 7.24 shows the corresponding analyses for 1st PC, along with the cognitive tests controlling for 1st PC and SIMPLE-RT. In this case, two cognitive tests (but not 1st PC) showed statistically significant positive differences (WCST-PERS and (SENTENCE-VERIF), but in neither case did this occur in the group with the largest BRAINVOL difference. Table 7.25 shows the same analyses for MENARCHE, THROW, and the sociality measures. None of the t-values are very large, and none are significant. MENARCHE consistently shows the reverse pattern from that predicted by the between-species primate data. However, only three of the variables in this table showed negative t-values in the group with the largest BRAINVOL differences.

Overall, these analyses confirm, using a simpler methodology, a lack of association between behavioral variables and overall brain size within families.

7.11 Linguistic Variables

This study used linguistic tasks that differ in some important ways from those used in other studies, and it is of interest to review specific findings related to these tasks for the benefit of future research. The average median time to verify that a simple object correctly matched its descriptive name (OBJECT-ID) was 682 ms (±157) across all subjects, which was 392 ms longer than it took the subjects to respond to a simple stimulus change (SIMPLE-RT) using the same apparatus (average median SIMPLE-RT was 290 ms; see table 6.4). The average median time to verify that a right-branching sentence correctly matched a picture was 3522 ms, while center-embedded

Table 7.24: Average within-family differences for the First PC and the other cognitive variables controlling for First PC grouped by within-family BRAINVOL differences

Sibling

BRAINVOL Mean Difference

Variable1 Difference2 N on Variable3 SD t-Value4 Probability5

1st PC largest 12 .06 1.30 .16 NS

middle 12 -.05 .88 -.18 NS

smallest 12 .14 .84 .60 NS

VOCAB largest 12 1.65 7.05 .81 NS middle 12 2.04 5.13 1.38 p<.10 smallest 12 -1.45 3.39 -1.48 NS

RAVEN largest 12 -.10 4.06 -.08 NS middle 12 .16 3.56 .16 NS smallest 12 1.25 3.01 1.44 p<.10

MRT-SPEED largest 12 -.29 .42 -2.39 NS middle 12 -.01 .35 -.10 NS smallest 12 .03 .43 .23 NS

MRT-N largest 12 .62 4.28 .50 NS middle 12 .64 3.69 .60 NS smallest 12 -.22 3.76 -.21 NS

STROOP largest 12 1.40 9.85 .49 NS middle 12 -.11 6.05 -.06 NS smallest 12 .98 12.19 .28 NS

TRAILS largest 12 -.51 7.23 -.24 NS middle 12 -1.95 9.37 -.72 NS smallest 12 -.07 8.13 -.03 NS

VERBALFL largest 12 -1.07 10.65 -.35 NS middle 12 -2.10 7.86 -.93 NS smallest 12 1.71 8.65 .68 NS

WCST-PERS largest 12 -.64 13.10 -.17 NS middle 12 8.18 14.76 1.92 p<.05 smallest 12 -.36 14.43 -.09 NS

OBJECT-ID largest 12 -34.66 143.70 -.84 NS middle 12 -14.60 132.85 -.38 NS smallest 12 -57.18 129.52 -1.53 NS

SENTENCE-VERIF largest 12 195.33 886.81 .76 NS middle 12 321.91 595.07 1.87 p<.05 smallest 12 -83.33 420.79 -.69 NS

SYNTAX largest 12 285.75 1317.81 .75 NS middle 12 141.31 853.49 .57 NS smallest 12 220.33 448.57 1.70 p<.10

11st PC is independent of age and SIMPLE-RT. Other variables controlled for age, SIMPLE-RT, and 1st PC

3Mean of (larger-brained sister's score) - (smaller brained sister's score) for each variable

4(Mean Difference)/

5One-tailed

Table 7.25: Average within-family differences for MENARCHE, THROW, and sociality variables grouped by within-family BRAINVOL differences

Sibling

BRAINVOL Mean Difference

Variable1 Difference2 N on Variable3 SD t-Value4 Probability5

MENARCHE largest 12 -.46 .89 -1.80 NS middle 12 -.15 1.25 -.41 NS smallest 11 .29 1.58 .61 NS

THROW largest 12 1.14 4.85 .82 NS middle 12 -2.51 3.78 -2.30 NS smallest 12 -.31 3.54 -.30 NS

Sociality measures:

ADDRESS BOOK largest 12 8.11 53.75 .52 NS

TOTAL middle 12 -8.95 57.51 -.54 NS

smallest 12 .97 40.37 .08 NS

ADDRESS BOOK largest 12 .19 6.12 .11 NS

RELATIVES middle 12 2.16 7.89 .95 NS

smallest 12 -.42 6.91 -.21 NS

PEOPLE SEEN largest 12 3.61 25.49 .49 NS

SOCIALLY middle 12 .45 9.08 .17 NS

smallest 12 -3.51 8.38 -1.45 NS

PEOPLE TALKED largest 12 -.06 60.38 .00 NS

TO middle 12 -.86 53.58 -.06 NS

smallest 12 -10.01 35.38 -.98 NS

SELF RATING largest 12 -.27 1.51 -.63 NS

middle 12 -.17 1.24 -.48 NS

smallest 12 .08 1.32 .22 NS

RATING BY largest 12 -.25 1.54 -.56 NS

SIBLING middle 12 -.48 1.47 -1.13 NS

smallest 12 -.48 1.23 -1.36 NS

SOCIALITY 1st PC6 largest 12 .16 1.35 .40 NS

middle 12 .05 .91 .19 NS

smallest 12 -.17 .69 -.87 NS

1Corrected for age. THROW is also corrected for SIMPLE-RT

3Mean of (larger-brained sister's score) - (smaller brained sister's score) for each variable

4(Mean Difference)/

5One-tailed

6Based on first four sociality measures only (see text)

sentences took an average median time of 4214 ms (table 6.4). Thus, since the only difference between these two sets of sentences was in the order of the words used, their difference of 692 ms in average median decision times (which is highly significant: paired t-test p< 0.0001) can only be attributable to the specific effects of syntax (hence the variable name: SYNTAX). However, this difference shows substantial variation across subjects that cannot be ascribed solely to chance.[14] In fact, there was substantial individual variability in all three linguistic tasks (table 6.4). On OBJECT-ID the range in median verification times went from 364 to 1026 ms. The range for right-branching sentence median verification times went from 2030 to 8652 ms, and for center-embedded sentences the times ranged from 2358 to 8152 ms. Thus, there is significant individual variation on these linguistic tasks, including variability that is due solely to syntactical differences in the sentences.

There are two major reasons why subjects might differ on the speed at which they process the two types of syntactic constructions. It could be that these forms do actually differ in their cognitive processing demands, and that individuals differ in their ability to process them. Alternatively, it might be that there are significant individual differences in the amount of past exposure to the two forms, such that some subjects respond slower on one type because they have had significantly less practice processing them. There are several indications in the present data, however, that this latter explanation is not sufficient. If the amount of past exposure were crucial, one might expect that SYNTAX should correlate strongly with SENTENCE-VERIF. However, the correlation, both within and between families, is low (though it does almost reach significance at the p< 0.05 level between families; see tables 7.7 and 7.8). Additionally, one would expect to find significant correlations between SYNTAX and a number of other variables that are likely indicators of the degree of past exposure to complex syntactical forms. Examples include: VOCAB, VERBALFL, SES, and the years in school of the parents and the subject: SCHOOL-S, SCHOOL-M, SCHOOL-F. Table 7.26 shows the correlations between SYNTAX and each of these variables both between and within families. None of them is close to significance. Furthermore, a multiple regression involving all these variables succeeds in explaining only nine percent of the variance in SYNTAX between families, and only three percent within families (the multiple correlations are not statistically significant). Even after adjusting for the fact that the reliability of SYNTAX is not high (though still very significant: see footnote 42), less than 25 percent of the reliable (i.e., non-error) variance in SYNTAX can be explained by these measures.[15]

Overall, SYNTAX does seem to be strongly associated with other cognitive dimensions. Between families, SYNTAX correlated significantly only with RAVEN, though it just missed significance with SENTENCE-VERIF as mentioned above (table 7.7). Within families none of its associations with other cognitive variables reached significance (table 7.8). These facts are reflected in the moderate loadings SYNTAX has on the

Table 7.26: Between and within family associations between SYNTAX and six possible correlates of past exposure to esoteric syntax1

Between Within2

VOCAB .17 .19

VERBALFL .10 .04

SCHOOL-S -.01 -.02

SCHOOL-M .10

SCHOOL-F .10

SES .18

Multiple r .30 .19

Multiple r2 .09 .03

* p<.05, ** p<.01

1VOCAB and VERBALFL are corrected for age and SIMPLE-RT;

SCHOOL-S, SCHOOL-M, and SCHOOL-F are corrected for age only.

2Multiple r within families does not include SES, SCHOOL-M, or

SCHOOL-F, which are solely between family variables.

between-family cognitive 1st PC, and the small loading it has on the within-family cognitive 1st PC (see tables 7.10 and 7.12). Thus it would appear that whatever cognitive demands SYNTAX places on the subjects, it is substantially independent of general cognitive ability. The possible significance of this will be addressed in the next chapter.

SENTENCE-VERIF (the average of right-branching and center-embedded sentence verification times) consistently showed among the highest loadings of all cognitive tests with the 1st PC (tables 7.10 and 7.12). It correlated significantly with RAVEN between families, and just missed significance (uncorrected for multiple comparisons) within families (compare tables 7.7 and 7.8). It correlated significantly with VOCAB between families, as one might expect, but a substantial portion of this correlation does not appear to be due to an intrinsic (direct causal) association between the two, since the within family correlation is not significant (however, see discussion in the next chapter about the possibility of within-family environmental effects masking any intrinsic relationship). SENTENCE-VERIF has both a linguistic and a spatial component, yet correlates most highly (between-families) with the non-verbal reasoning test: the RAVEN. The RAVEN test does potentially have a spatial component as well, in that the subject is looking at patterns which differ in their (two-dimensional) spatial characteristics.

The speed at verifying whether a single word matches an object (OBJECT-ID) showed only moderate (and non-significant) correlations with other cognitive tests, with the exception of SENTENCE-VERIF between and within families and SIMPLE-RT between families only (tables 7.7 and 7.8). The absolute magnitude of the average OBJECT-ID bears an interesting relationship with the more complex sentence verification tasks. If we subtract the average median SIMPLE-RT value from the average values of OBJECT-ID and both right-branching and center-embedded sentence median verification times, we get the following:

OBJECT-ID: 392 ms

right-branching sentence: 3232 ms

center-embedded sentence: 3924 ms

These represent estimates of the actual processing times independent of the basic reaction processes common to all three tasks. Thus, the right-branching sentences, which are 11 words long, take only ~ 8.25 times longer to process than single concrete nouns. The center-embedded sentences used in this study, also 11 words long, take ~10 times as long. Three of the 11 words in these sentences are the article "the", which probably requires very little processing time. If so, the time required to process a right-branching sentence is reasonably well predicted given the time needed to process a single word, whereas center-embedded sentences take longer than a simple model predicts. The possible significance of this will be discussed in the next chapter.

[1]Body size correction was accomplished by using the residuals of a multiple regression of the neuroanatomical variable with both BODY-WT and SIT-HT. This results in neuroanatomical variables that are uncorrelated with both BODY-WT and SIT-HT. SIT-HT was used instead of BODY-HT because SIT-HT is more highly correlated with the neuroanatomical variables than is BODY-HT (see Tables 7.5 and 7.6). The results indicate that on average these body-size corrected neuroanatomical variables result in correlations that differ by only a few points. For example, the correlation between the 1st PC and BRAINVOL (body size corrected) between families is only .01 less than the same correlation using BRAINVOL uncorrected for body size. Similarly, the within family correlation between the 1st PC and BRAINVOL (body size corrected) is only .02 larger than the corresponding correlation using BRAINVOL uncorrected for body size. These obviously have no meaningful effect on the conclusions presented here.

[2]These significance levels where not corrected for multiple comparisons for the reasons outlined at the end of the previous chapter.

[3]However, this is not true for every behavior. If the behavior tends to induce the individual to have decreased fitness, then a negative correlation would not be a problem.

[4] Including SELF RATING and RATING BY SIBLING in the calculation of the between family SOCIALITY 1st PC reduces its correlation with BRAINVOL to just below the p < .05 level (r = .31), but it remains significant for MMMVOL (r = .42).

[5]On the assumption that the correlations are approximately normally distributed, and that each cognitive test represents an independent replication.

[6]Estimates of the within- and between-family standard deviations for BRAINVOL were derived by taking the square-root of the mean squares in an ANOVA with sibling pairs as groups. This was done using BRAINVOL uncorrected for age or SRT.

[7]Using the appropriate formulas in Jensen (1980): rbetween (corrected for attenuation) = (rbetween)/[(rX(between))(rY(between))]1/2; in which rX(between) = (rXX + rXsibs)/(1 + rXsibs), andrY(between) = (rYY+rYsibs)/(1 + rYsibs). In these formulas rXX = reliability of variable X, rXsibs = the intraclass correlation between siblings on variable X, rYY = reliability of variable Y, and rYsibs = the intraclass correlation between siblings on variable Y.

[8]Using formula 14.30 (p. 343) from Guilford (1965): r (corrected for range restriction) = [r (sU/sR)]/[1 - r2 + r2 (s2U/s2R)]1/2, where sU = standard deviation of the variable in the non-range-restricted group, and sR = standard deviation of the same variable in the range-restricted group. This formula assumes a truncation of the variance at one end of the distribution, but there would appear to be no a priori reason why this sort of range-restriction should have markedly different effects on correlations than the present case. Also note that the formula uses an estimate of range restriction from only one variable.

[9]Using the inverse of the appropriate formulas in Jensen (1980): rwithin (attenuated) = (rwithin )/[(rX(within))(rY(within))]1/2; in which rX(within) = (rXX - rXsibs)/(1 - rXsibs), andrY(within) = (rYY - rYsibs)/(1 - rYsibs). As with footnote 36, in these formulas rXX = reliability of variable X, rXsibs = the intraclass correlation between siblings on variable X, rYY = reliability of variable Y, and rYsibs = the intraclass correlation between siblings on variable Y.

[10]The standard deviation of these differences is of this magnitude because the variability in the size of correlations based exclusively on random variation is not trivial. With an N of 36, only a correlation of r³0.33 is statistically significant at the p<0.05 level. This means that 95% of the time correlations based exclusively on random variation will fall between -0.33<r<+0.33, thus the standard deviation of 0.237 is quite reasonble.

[11]The average "within-family" correlation was -.007 (SD = .165). 807 trials (p= .807) resulted in a "within-family" correlation of ³ ±.04 (the empirical finding in the present study for BRAINVOL to 1st PC within families).

[12]The average within group correlation was r = .19 (s = .12), and the average between group correlation was r = .30 (s = .13). These correlations are actually both, in effect, between family comparisons because the groups used to calculate the within and between group correlations were of course not family pairs. It is not clear why these within and between group correlations should be lower than the actual between family correlation. It might be explained if we assume that there are between family environmental influences which contribute to the between family correlation. These influences would be randomized by non-family groupings, and hence would tend to cancel out.

[13]Except for SIMPLE-RT itself, of course, which is only controlled for age.

[14]The two sentence types correlate r= .85, which, though high, is significantly less than r= 1.00 (95% intervals run from .76 to .90). Thus, there is some significant amount of variation in one that cannot be explained by variation in the other. Also, the internal reliability of the SYNTAX measure (center-embedded RT minus right-branching RT) is r= .53, which is significant at the p< .01 level.

[15]Reliability between and within families was estimated using the formulas 1 and 2 in Jensen (1980), which require reliability estimates and intraclass correlations for the variables. Reliability for SYNTAX was taken from table 6.11, reliability for the six other measures was assumed to average r= .90. Intraclass correlations were calculated from F ratios of between vs. within family variance (the result of an ANOVA with sibling pairs as groups).